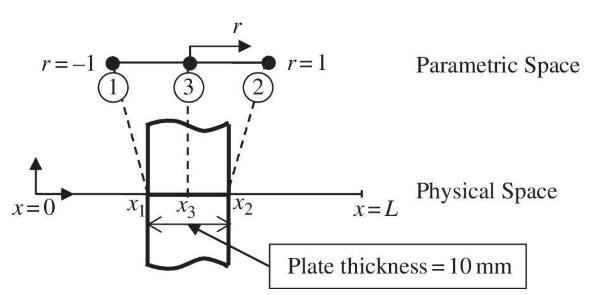
The heat conduction through the thickness of a plate can be modeled as a single 1D quadratic (3node) element assuming that the plate is large with uniform temperature on the same thickness. The temperature at \(x_{1}\) is fixed at \(100{ }^{\circ} \mathrm{C}\) while \(x_{2}\) is at \(25^{\circ} \mathrm{C}\). Heat is being generated within the plate at the rate of \(Q_{g}=1000 \mathrm{~W} / \mathrm{m}^{3}\). The conductivity of the plate is \(k=5.2 \times 10^{-2} \mathrm{~W} /\left(\mathrm{mm}^{\circ} \mathrm{C}ight)\), and the thickness of the plate is \(10 \mathrm{~mm}\). When the shape functions and conductivity matrix are given,

a. compute the nodal equivalent heat source corresponding to the heat generation in the plate.

b. determine the temperature distribution \(T(r)\). Note \(k\) is conductivity, \(A=\) area, \(L^{(e)}=\) length of the element.

Transcribed Image Text:

r=-1 r=1 Parametric Space 1 3 2 x=0 X1 X3 X2 Physical Space x=L Plate thickness = 10 mm