To apply Chang and Roberts’ election algorithm to a hypercube one can first generate a spanning ring in the given hypercube (see the figure below for a 3-dimensional hypercube example.)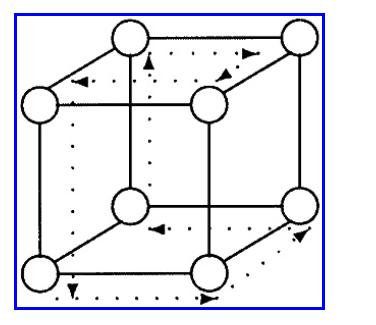

Assume that one process initiates an election process at a time. In the worst case, almost 2 rounds are needed to elect a winner. Enhance Chang and Roberts’ algorithm to obtain a faster election process for the hypercube topology by using multiple paths provided by the hypercube. Assume that each node can send a message to multiple neighbors simultaneously. Only a high-level description of your algorithm is needed. Use the 3-dimensional hypercube example to illustrate your approach.