(a) Consider complex power transmission via the three-phase long line for which the per-phase circuit is shown...
Question:
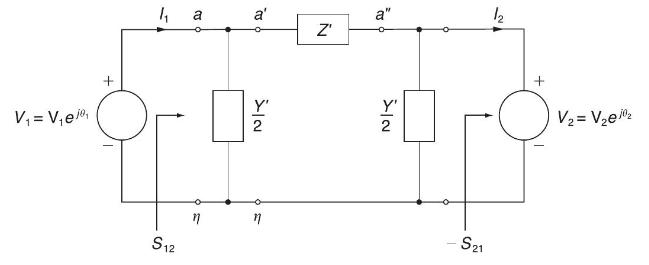
(a) Consider complex power transmission via the three-phase long line for which the per-phase circuit is shown in Figure 5.20. See Problem 5.37 in which the short-line case was considered. Show that
\[
\begin{aligned}
& \text { sending-end power }=S_{12}=\frac{Y^{*}}{2} \mathrm{~V}_{1}^{2}+\frac{\mathrm{V}_{1}^{2}}{Z^{\prime *}}-\frac{\mathrm{V}_{1} \mathrm{~V}_{2}}{Z^{\prime *}} e^{j \theta_{12}} \\
& \text { received power }=-S_{21}=-\frac{Y^{\prime *}}{2} \mathrm{~V}_{2}^{2}-\frac{\mathrm{V}_{2}^{2}}{Z^{\prime *}}+\frac{\mathrm{V}_{1} \mathrm{~V}_{2}}{Z^{\prime *}} e^{-j \theta_{12}}
\end{aligned}
\]
where \(\theta_{12}=\theta_{1}-\theta_{2}\).
(b) For a lossless line with equal voltage magnitudes at each end, show that
\[
P_{12}=-P_{21}=\frac{V_{1}^{2} \sin \theta_{12}}{Z_{c} \sin \beta \ell}=P_{S I L} \frac{\sin \theta_{12}}{\sin \beta \ell}
\]
(c) For \(\theta_{12}=45^{\circ}\) and \(\beta=0.002 \mathrm{rad} / \mathrm{km}\), find \(\left(\mathrm{P}_{12} / \mathrm{P}_{\mathrm{SIL}}ight)\) as a function of line length in \(\mathrm{km}\), and sketch it.
(d) If a thermal limit of \(\left(\mathrm{P}_{12} / \mathrm{P}_{\text {SIL }}ight)=2\) is set, which limit governs for short lines and long lines?
Problem 5.37
(a) Consider complex power transmission via the three-phase short line for which the per-phase circuit is shown in Figure 5.19. Express \(S_{12}\), the complex power sent by bus 1 (or \(V_{1}\) ), and \(\left(-S_{21}ight.\) ), the complex power received by bus 2 (or \(V_{2}\) ), in terms of \(\mathrm{V}_{1}, \mathrm{~V}_{2}, \mathrm{Z}, \angle Z\), and \(\theta_{12}=\) \(\theta_{1}-\theta_{2}\), which is the power angle.
(b) For a balanced three-phase transmission line in per-unit notation with \(Z=1 \angle 85^{\circ}, \theta_{12}=10^{\circ}\), determine \(S_{12}\) and \(\left(-S_{21}ight)\) for (i) \(\mathrm{V}_{1}=\mathrm{V}_{2}=1.0\)
(ii) \(\mathrm{V}_{1}=1.1\) and \(\mathrm{V}_{2}=0.9\)
Comment on the changes of real and reactive powers from parts (i) to (ii).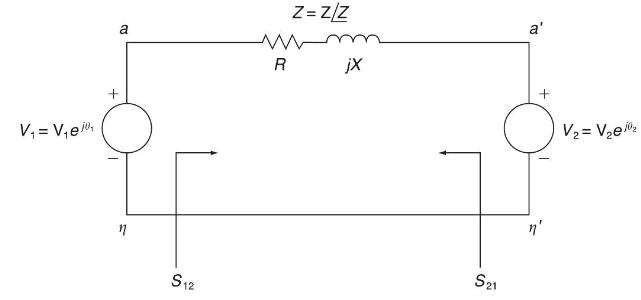
Step by Step Answer:

Power System Analysis And Design
ISBN: 9781305632134
6th Edition
Authors: J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma




