For the single-phase line of Problem 4.14 (b), if the height of the conductor above ground is
Question:
For the single-phase line of Problem 4.14
(b), if the height of the conductor above ground is \(80 \mathrm{ft}\)., determine the line-to-line capacitance in \(\mathrm{F} / \mathrm{m}\). Neglecting earth effect, evaluate the relative error involved. If the phase separation is doubled, repeat the calculations.
Problem 4.14
(a) In practice, one deals with the inductive reactance of the line per phase per mile and use the logarithm to the base 10. Show that Eq. (4.5.9) of the text can be rewritten as
\[
\begin{aligned}
x & =k \log \frac{\mathrm{D}}{r^{\prime}} \text { ohms per mile per phase } \\
& =x_{d}+x_{a}
\end{aligned}
\]
where \(x_{d}=k \log \mathrm{D}\) is the inductive reactance spacing factor in ohms per mile \(x_{a}=k \log \frac{1}{r^{\prime}}\) is the inductive reactance at 1 -ft spacing in ohms per mile \(k=4.657 \times 10^{-3} f=0.2794\) at \(60 \mathrm{~Hz}\)
(b) Determine the inductive reactance per mile per phase at \(60 \mathrm{~Hz}\) for a single-phase line with phase separation of \(10 \mathrm{ft}\) and conductor radius of \(0.06677 \mathrm{ft}\). If the spacing is doubled, how does the reactance change?
Eq. (4.5.9)
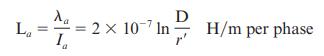
Step by Step Answer:

Power System Analysis And Design
ISBN: 9781305632134
6th Edition
Authors: J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma





