The capacitance-to-neutral, neglecting the ground effect, for the threephase, single-circuit, bundle-conductor line is given by

\[
\begin{gathered}
\mathrm{C}_{a \eta}=\frac{2 \pi \varepsilon_{0}}{\ell \eta\left(\frac{\mathrm{GMD}}{\mathrm{GMR}}ight)} \mathrm{F} / \mathrm{m} \text { line-to-neutral } \\
\text { Where GMD }=\left(\mathrm{D}_{A B} \mathrm{D}_{B C} \mathrm{D}_{A C}ight)^{1 / 3} \\
\mathrm{GMR}=\left[r N(\mathrm{~A})^{N-1}ight]^{1 / N}
\end{gathered}
\]

in which \(N\) is the number of subconductors of the bundle conductor on a circle of radius A, and each subconductor has an outside radius of \(r\). The capacitive reactance in mega-ohms for \(1 \mathrm{mi}\) of line at \(60 \mathrm{~Hz}\) can be shown to be \(\mathrm{X}_{C}=0.0683 \log \left(\frac{\mathrm{GMD}}{\mathrm{GMR}}ight)=\mathrm{X}_{a}^{\prime}+\mathrm{X}_{d}^{\prime}\)
where \(\mathrm{X}_{a}^{\prime}=0.0683 \log \left(\frac{1}{\mathrm{GMR}}ight)\) and \(\mathrm{X}_{d}^{\prime}=0.0683 \log (\mathrm{GMD})\).
Note that A is related to the bundle spacing \(S\) given by \[
\mathrm{A}=\frac{S}{2 \sin \left(\frac{\pi}{N}ight)} \quad \text { for } N>1 \]
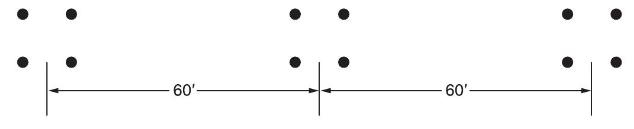
Using the above information for the configuration shown in Figure 4.40, compute the capacitance-to-neutral in \(\mathrm{F} / \mathrm{m}\) and the capacitive reactance in \(\Omega \cdot\) mi to neutral for the three-phase, \(765-\mathrm{kV}, 60-\mathrm{Hz}\), single-circuit, bundle-conductor line \((N=4)\) with subconductor's outside diameter of 1.16 in. and subconductor spacing \((S)\) of 18 in.

60'- 60'