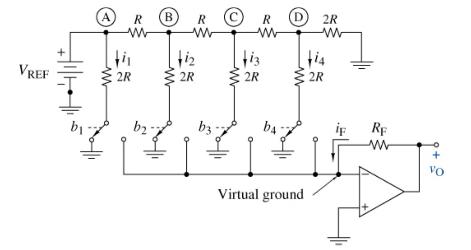
The circuit in Figure P4=76 is a four-bit DAC. The DAC output is the voltage \(v_{\mathrm{O}}\) and the input is the binary code represented by bits \(b_{1}, b_{2}, b_{3}\), and \(b_{4}\). The input bits are either \(\mathrm{o}\) (low) or 1 (high), and each controls one of the four switches in the figure. When bits are low, their switches are in the left position, directing the \(2 R\) leg currents to ground. When bits are high, their switches move to the right position, directing the \(2 R\) leg currents to the OP AMP's inverting input. The 2R leg currents do not change when switching from left to right because the inverting input is a virtual ground \(\left(v_{\mathrm{N}}=v_{\mathrm{P}}=0ight)\). The purpose of this problem is to show that this constant-current switching produces the following input-output relationship.
\[
v_{\mathrm{O}}=-\frac{R_{\mathrm{F}}}{2 R} V_{\mathrm{REF}}\left(b_{1}+\frac{b_{2}}{2}+\frac{b_{3}}{4}+\frac{b_{4}}{8}ight)
\]
(a) Since the inverting input is a virtual ground, show that the currents in the \(2 R\) legs are \(i_{1}=V_{\mathrm{REF}} / 2 R, i_{2}=V_{\mathrm{REF}}\) \(/ 4 R, i_{3}=V_{\mathrm{REF}} / 8 R\), and \(i_{4}=V_{\mathrm{REF}} / 16 R\), regardless of switch positions.
(b) Show that the sum of currents at the inverting input is \[
b_{1} i_{1}+b_{2} i_{2}+b_{3} i_{3}+b_{4} i_{4}+i_{\mathrm{F}}=0
\]
where bits \(b_{\mathrm{k}}(k=1,2,3,4)\) are either \(\mathrm{o}\) or 1 .
(c) Use the results in parts (a) and (b) to show that the OP AMP output voltage is as stated above.

Transcribed Image Text:

VREF b A R w www 2R b B) www R www fiz 2R b3 R www 2R D ww Virtual ground 2R www 2R RE VO