Question: Consider a network given by the adjacency matrix a ij = a ji = 1 with probability p and a ij = a ji =

Consider a network given by the adjacency matrix a_ij = a_ji = 1 with probability p and a_ij = a_ji= 0 with probability 1 − p.
(a) In the limit of large N and fixed pN, compute the degree distribution and calculate the connectivity.
(b) Now exclude the nodes of degree zero and neglect degree correlations. Use the distribution derived in (a) in the limit of large N and Np fixed to express the average return time r_i for the nodes of non-zero degree in terms of Ei(pN), where Ei(pN) denotes the exponential integral.

(c) Compare the expression in (b) with the estimate one obtains by the definition of r_i in Eq. (8.99), replacing k_i by the average degree and L by the average number of links. Consider the limit Np → 0 and N ≫ 1.

Eq. (8.99)

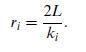
2L ki

Step by Step Solution

★★★★★

3.45 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related The Physics Energy Questions!

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

You get a summer job with a company which has an in-house operating system called sOs. sOs uses static priority scheduling, supports at most 32 concurrently-executing processes, and works only on...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

**Make sure to present the output within a proper message. For example, assume that you are asked to find the rank of a matrix. Do not just print the number that represents its rank. You need to show...

Solve this problem using Matlab. Solve this problem using Matlab. Handwriten Solution are not accebtable Thank you. 2 Part 2-Network Application: The Adjacency Matrix of a Graph 2.1 Introduction...

CMPE 107 Spring 2016 Take-Home Exam MUST BE SUBMITTED IN HARD COPY BY JUNE 7 NO LATER THAN 4PM [in JJ's office or with Ali in E2 315] Grading system: presentation = 25%, content = 75% Last Name:...

1.14 ( ) Show that an arbitrary square matrix with elements wij can be written in the form wij = wS ij + wA ij where wS ij and wA ij are symmetric and anti-symmetric matrices, respectively,...

Submit written solutions to the following exercises. Remember that weekly homework assignments will be graded carefully for correctness, completion, and clarity of reasoning. In order to receive full...

Attached slide 6 Consider the following Stochastic Block Model (SBM) specified by the following parameters: 7r:(.5 .15 .35) .9 .15 .25 B : .15 .75 .05 .25 .05 .6 p : 1 For all plots for this...

For all plots for this question, it is not necessary to include axis labels. Include a legend where the values plotted are non-binary. Always include a title. Additionally, for all heatmap" style...

The commercial banking industry in Canada is less competitive than the commercial banking industry in the United Stated because in Canada only a few large banks dominate the industry, while in the...

Yttria (Y2O3) particles 750 in diameter are introduced into tungsten by internal oxidation. Measurements using an electron microscope show that there are 5 1014 oxide particles per cm3. Calculate...

Meger: 1 9 8 Frag thits pege 8 . Nancy lives in Abitibi and is proud to contribute to local economic development. She has invested a large part of her savings ( $ 1 0 0 , 0 0 0 ) in the stocks of...

Which of the following could explain why accounting is more conservative in some countries than in others? LO4 a. Accounting is oriented toward stockholders as a major source of financing. b....

Verify the assertion made in 13.5.2 that the net efficiency of a CCGT is net = B + R (1 B ), where B/R is the efficiency of the Brayton/Rankine cycle.

A rocket fuel should have high energy density (per kilogram) because the weight of the propellant is an important consideration. A favorite fuel is liquid hydrogen plus liquid oxygen. What is the...

In principle, and in the absence of electromagnetic or any other non-gravitational interactions, an electron and a proton should form a ?gravitational atom,? bound by the force of gravity. We know...

Question 6 5 pts Pollo Inc.'s 5.57% bonds have a YTM of 12.31%. The estimated risk premium between the company's bonds and stocks is 4%. Pollo's cost of common equity, Re, is ____%. Round your final...

Write a program that will accepts two integers. The two integers represent the dividend and divisor of the program. Compute and display the quotient and remainder.

5. You work for a furniture store. You normally sell a living room set for $4,000 and finance the full purchase price for 24 monthly payments at 24% APR. You are planning to run a zero-interest...