Consider a random walker on the set of non-negative integers {0,1,2, . . .}. The probability of a step to the right is p+ and of a step to the left is p−, and p+ = p− = 1/2.
Assume that the site x = 0 is an absorbing sink (i.e. the probability of moving from x = 0 to x = 1 is zero) and that P(1,0) = 1, i.e. at time zero the walker starts at position x = 1.
(a) Express the probability P_R(T) that the walker arrives at zero for the first time in terms of P(1,t). Note: P_R(T) is called the first return time probability.
(b) Iterate the master equation for P(x,t) in order to numerically determine P_R(T) and determine the functional dependence on T for large T.You can compare your result to the graph in Fig. 10.13.

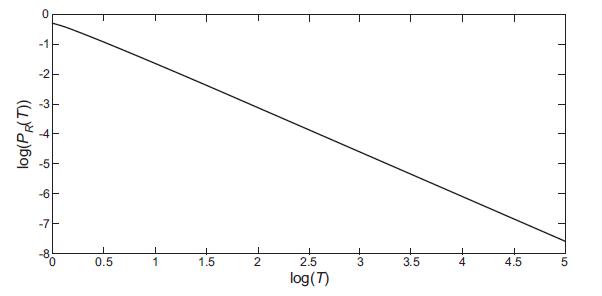
(c) Next consider the continuum limit of the master equation and determine the probability for first return at time T from the gradient (current) at position x → 0+.

Transcribed Image Text:

log(PR(T)) + T 0 0.5 1 1.5 12 2.5 log(7) 3.5 45