In 29.4.1 it is asserted that eq. (29.28) describes the steady, circulation-free flow of an incompressible ideal
Question:
In §29.4.1 it is asserted that eq. (29.28)
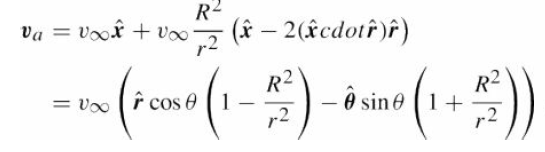
describes the steady, circulation-free flow of an incompressible ideal fluid around a cylinder. To confirm this, verify
(a) that va → v∞ x̂ as r → ∞;
(b) that no fluid flows into or out of the cylinder;
(c) that the circulation is zero around any circle of radius r > R;
(d) that ∇ × va = 0 (zero vorticity) and ∇ · v∞ = 0 (incompressibility) everywhere outside the cylinder. For part (d) va can be written as the gradient of a scalar function, va = ∇Φ, where
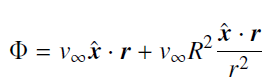
Also make use of the identities eq. (B.18)
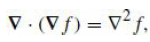
and eq. (B.20)
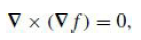
, and the facts that ∇(1/rp) = −pr̂/rp+1 and ∇2(1/rp) = p2/rp+2. The identity ∇2( f g) = f ∇2g + g∇2 f + 2∇f · ∇g may be useful as well.
R- (& – 2(fcdotf)f) va = vooê + vo m(tcme (1-) R- - ê sine (1+ r2 = vo (î cos 0 ( 1 -2 D = v„ê · r + vR²*," r2
Step by Step Answer:
a Since the second term in the first form of eq 292...View the full answer



Related Video
The area of a circle is given by the formula: A = ?r^2 Where A is the area, ? is a mathematical constant (approximately 3.14), and r is the radius of the circle. The radius is the distance from the center of the circle to the edge. So for example, if the radius of a circle is 5 units, the area would be: A = ?(5^2) = ?(25) = 78.5 square units Here three friends went out to a restaurant and decided to have pizza for lunch. While they were waiting for their order, one of them stepped out to take a call but promised to return in two minutes. The waiter came and presented them with the menu, and they decided to order two 10-inch pepperoni pizzas. The waiter took their order and left. Just then, the third friend returned and asked what they had ordered. They explained that they had ordered two small pepperoni pizzas as they were only three of them and it would be enough for them. However, the third friend suggested that for the same price, they could get a large pizza that would be much bigger than the two small ones. He asked the waiter for a pen and paper and proceeded to calculate the area of the two small pizzas and compared it to the area of one large pizza. The friends were amazed at how the circle measurements worked and decided to change their order from two small pizzas to one large pizza.
Students also viewed these Physics questions
-
In Section 8.6, it was asserted that the sum of all the internal torques (that is, the torques due to internal forces) acting on a rigid object is zero. The figure shows two particles in a rigid...
-
Steady potential flow around a stationary sphere. 2 In Example 4.2-1 we worked through the creeping flow around a sphere. We now wish to consider the flow of an incompressible, inviscid fluid in...
-
The flow field about a line source considers the symmetric radial flow of an incompressible, inviscid fluid outward from an infinitely long uniform source, coincident with the z-axis of a cylindrical...
-
Find the lengths of the curves. The cardioid r = 1 + cos
-
The article "The Respiration in Air and in Water of the Limpets Patella caerulea and Patella lusitanica" (Comp. Biochemistry and Physiology, 1975: 407-411) proposed a simple power model for the...
-
Briefly describe some ways that companies have used the Internet as a new customer service support channel.
-
Explain the positive classification criterion.
-
Multiple Choice Questions 1. Walters, an individual, received the following in 2016: W-2 income .........................................................................$10,000 Federal tax refund for...
-
The following is the adjusted trial balance for Stockton Company. d. $1,100 b. $23,406 c. $28,993 d. $21,336
-
In an interview published in the New York Times in February 1976, former Lockheed president A. Carl Kotchian defended the payment of bribes by the company as follows: Some call it gratuities. Some...
-
Suppose that in a region of steady flow the velocity of a fluid is given by v = r, where r is the vector from a fixed point in space. Describe the streamlines of this flow. Show that v = 0, so...
-
Investigate the location of the stagnation points for fluid flow around a cylinder as described in 29.4.1. Show that for small there are two stagnation points on the cylinder and find their...
-
A gas mixture containing 85.0 mole% N2 and the balance n-hexane flows through a pipe at a rate of 100.0m 3 fh, the pressure is 2.00 atm absolute and the temperature is 100C. (a) What is the molar...
-
Zephyr Minerals completed the following transactions involving machinery. Machine No. 1550 was purchased for cash on April 1, 2020, at an installed cost of $75,000. Its useful life was estimated to...
-
Kelly is a self-employed tax attorney whose practice primarily involves tax planning. During the year, she attended a three-day seminar regarding new changes to the tax law. She incurred the...
-
At a recently concluded Annual General Meeting (AGM) of a company, one of the shareholders remarked; historical financial statements are essential in corporate reporting, particularly for compliance...
-
4. In hypothesis, Mr. Ng wants to compare the solution in Q3 to other solutions in different conditions. If the following constraints are newly set in place, answer how much different is going to be...
-
3C2H6O2+7H2O= C2H4O3+11H2+O2+H2C2O4+CH2O2 Glycolic acid is produced electrochemically from ethylene glycol under alkaline conditions(NaOH). Hydrogen is produced at the cathode, and formic acid and...
-
In September 2020, Unilever and JP Morgan entered into a $500 million 10-year swap, the first swap to use SOFR as the reference interest rate. The interest rate swap effectively converted $500...
-
If there is an unrealized holding gain on available-for-sale investments, it is reported as?
-
If are the Fourier coefficients of a real signal, x(t), fill in all the steps to show that: (a) (b) X n is a real, even function of n for x(t) even. (c) X n is imaginary and an odd function of n for...
-
Expand the signal x(t) = 2t 2 in a complex exponential Fourier series over the interval |t| 2. Sketch the signal to which the Fourier series converges for all t.
-
Using the uniqueness property of the Fourier series, find exponential Fourier series for the following signals (f 0 is an arbitrary frequency): (a) x 1 (t) = sin 2 (2f 0 t) (b) x 2 (t) = cos(2f 0 t)...
-
*please calculate irr in excel
-
Which of the following would not be a period cost? Research and development Direct materials Office supplies Advertising costs
-
\ table [ [ Activity Cost Pool,Activity Measure,Total Cost,Total Activity ] , [ Machining , Machine - hours,$ 3 3 0 , 0 0 0 , 1 5 , 0 0 0 MHs ] , [ Machine setups,Number of setups,$ 3 0 0 , 0 0 0 , 5...

Study smarter with the SolutionInn App


