Show that the energy density on a string u(x, t), defined in eq.?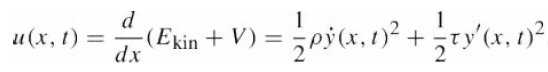

obeys the conservation law?u/?t +?S/?x = 0, where S (x, t) = ??y?y? is the energy flux, the energy per unit time passing a point x. For the traveling wave y(x, t) = f (x?vt), find u(x, t) and S (x, t) and show that energy flows to the right (for v > 0) as the wave passes a point x. Show that the total energy passing each point is equal to the total energy in the wave.

d (, 1) : dx (Exin + V) = p x.1 +y'a. n?