The project studies the paper [501]. Recall that the avalanche dynamics evolves on two time scales. The
Question:
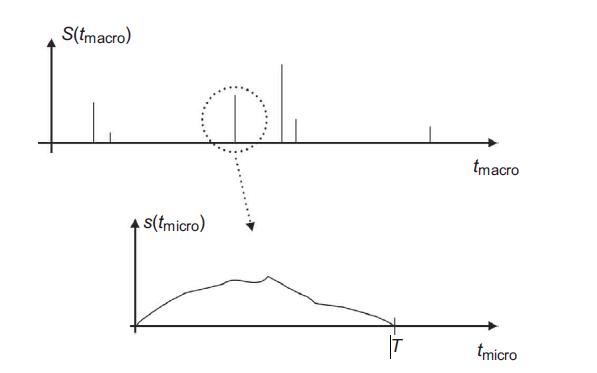
The project studies the paper [501]. Recall that the avalanche dynamics evolves on two time scales. The first, denoted by t, counts the numbers of energy units added to the pile.
In between each addition of an energy unit, the relaxation dynamics is allowed to run.
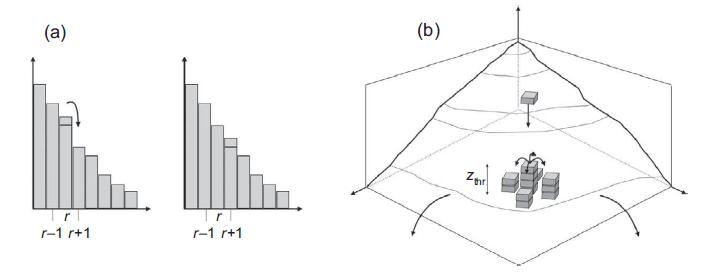
This is the branching process depicted in Fig. 1 of [501]. The relaxation probability p is kept constant while an avalanche spreads, which is described as a branching process. However, the adding of energy units and their escape at the boundary make the relaxation probability vary on the time scale t, hence Eq. (1), which is considered to represent the time dependence of p on the time scale of energy addition.
Figure 1.
Equation 1.

(a) Write down the branching probabilities for the process defined on p. 4071, bottom of the right column.
(b) Compute the generator function for the process and determine the average branching ratio from the generator. For which value pc of p is the process critical?
(c) Let τex denote the time to extinction. By use of generator formalism show that the probability


Step by Step Answer:

Complexity Science The Study Of Emergence
ISBN: 9781108834766
1st Edition
Authors: Henrik Jeldtoft Jensen





