(a) To compute the YTM for the 12-month note: which solves to YTM 1.91%. (b) Do...
Question:
(a) To compute the YTM for the 12-month note: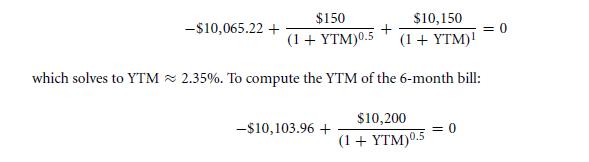
which solves to YTM ≈ 1.91%.
(b) Do it.
(c) The $150 coupon is worth $150/1.01910.5 ≈ $148.59. Therefore, the 1-year, zero note with one payment of $10,150 due in 1 year costs $10,065.22 − $148.59 = $9,916.63. This means that the 1-year, zero note with payoff of $10,150 has a YTM of $10,150/$9,916.63 − 1 ≈ 2.35%.
(d) Do it.
(e) The difference between the YTM of the coupon note (1.91%) and the zero note (235%) is only 0.44 basis points—very small, even though the yield curve here is fairly steep. The reason is that the early 6-month coupon (earning a lower interest rate) makes little difference because the coupon payment is only $150, and most of the YTM comes from the final payment. The coupon effect can become larger on very long horizons when the yield curve is steep, but it is very rarely more than 10–20 basis points.
Step by Step Answer:







