13. Let X1, X2, . . . be a sequence of independent random variables. The nonnegative integer valued random variable N is said to be a stopping time for the sequence if the event {N = n} is independent of Xn+1,Xn+2, . . . . The idea being that the Xi are observed one at a time—first X1, then X2, and so on—and N represents the number observed when we stop. Hence, the event {N = n} corresponds to stopping after having observed X1, . . . , Xn and thus must be independent of the values of random variables yet to come, namely, Xn+1,Xn+2, . . . .

(a) Let X1,X2, . . . be independent with

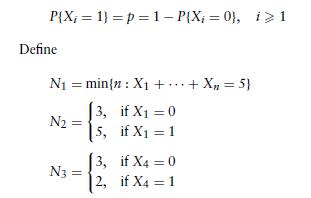
Which of the Ni are stopping times for the sequence X1, . . .? An important result, known as Wald’s equation states that if X1,X2, . . . are independent and identically distributed and have a finite mean E(X), and if N is a stopping time for this sequence having a finite mean, then

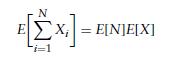
To prove Wald’s equation, let us define the indicator variables Ii , i 1 by

where the last equality assumes that the expectation can be brought inside the summation (as indeed can be rigorously proven in this case).

(c) Argue that Xi and Ii are independent.
Hint: Ii equals 0 or 1 depending on whether or not we have yet stopped after observing which random variables?

(d) From part

(c) we have

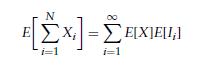
Complete the proof of Wald’s equation.

(e) What does Wald’s equation tell us about the stopping times in part (a)?

Transcribed Image Text:

P{X=1}=p=1-P{X=0}, i>1 Define N = min{n: X1+...+ X = 5} 3, if X10 N2 5, if X1=1 3, if X4 = 0 N3 = |2, if X4 1