82. Let X1,X2, . . . be independent continuous random variables with a common distribution function F and density f = F, and for k 1 let Nk = min{n k: Xn = kth largest of X1, . . . ,Xn}

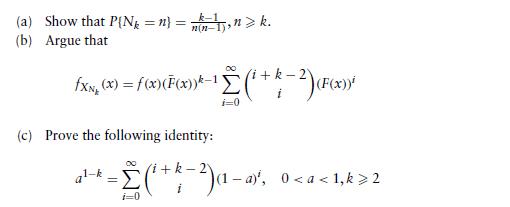
Hint: Use induction. First prove it when k = 2, and then assume it for k. To prove it for k + 1, use the fact that

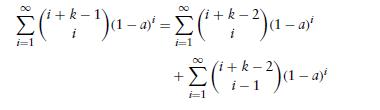
where the preceding used the combinatorial identity

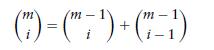
Now, use the induction hypothesis to evaluate the first term on the right side of the preceding equation.

(d) Conclude that XNk has distribution F.

Transcribed Image Text:

(a) Show that P{N = n} = n(n-1), ' k-1 ,nk. (b) Argue that fxx, (x) = f(x) (F(x))* (1+-2) (F(x)) (c) Prove the following identity: al-k == i=0 = (1 + k 2) (1 a)', i=0 a)', 0