Consider a graph with nodes 1, 2, . . . , n and the

n2

arcs (i, j ), i = j, i, j,=

1, . . . , n. (See Section 3.6.2 for appropriate definitions.) Suppose that a particle moves along this graph as follows: Events occur along the arcs (i, j ) according to independent Poisson processes with rates λij . An event along arc (i, j )

causes that arc to become excited. If the particle is at node i at the moment that

(i, j ) becomes excited, it instantaneously moves to node j, i, j = 1, . . . , n. Let Pj denote the proportion of time that the particle is at node j . Show that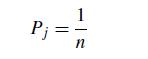

Hint: Use time reversibility.

- Pj n