Consider a Markov chain with states equal to the nonnegative integers, and suppose its transition probabilities satisfy Pi,j = 0 if j ≤ i. Assume X0 = 0, and let ej be the probability that the Markov chain is ever in state j . (Note that e0 = 1 because X0 = 0.) Argue that for j >0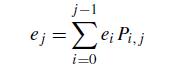

If Pi,i+k = 1/3, k = 1, 2, 3, find ei for i = 1, . . . , 10.

Transcribed Image Text:

j-1 ej =ei Pij i=0