Consider a particle that moves along a set ofm + 1 nodes, labeled 0, 1, . . . ,m, that are arranged around a circle (see Figure 2.3). At each step the particle is equally likely to move one position in either the clockwise or counterclockwise direction. That is, if Xn is the position of the particle after its nth step then

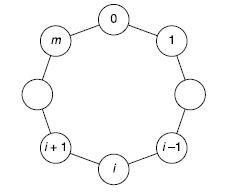
where i + 1 ≡ 0 when i = m, and i − 1 ≡ m when i = 0. Suppose now that the particle starts at 0 and continues to move around according to the preceding rules until all the nodes 1, 2, . . . ,m have been visited. What is the probability that node i, i = 1, . . . ,m, is the last one visited?

Transcribed Image Text:

P{Xn+1 = i + 1|Xn = i} = P{Xn+1 = i-1|X = i) =