Consider a Yule process starting with a single individualthat is, suppose X(0) = 1. Let Ti denote
Question:
Consider a Yule process starting with a single individual—that is, suppose X(0) = 1. Let Ti denote the time it takes the process to go from a population of size i to one of size i +1.
(a) Argue that Ti, i = 1, . . . , j, are independent exponentials with respective rates iλ.
(b) Let X1, . . . , Xj denote independent exponential random variables each having rate λ, and interpret Xi as the lifetime of component i. Argue that max(X1, . . . , Xj) can be expressed as max(X1, . . . , Xj) = ε1 + ε2 +· · ·+εj where ε1, ε2, . . . , εj are independent exponentials with respective rates jλ, (j −1)λ, . . . , λ.
Hint: Interpret εi as the time between the i −1 and the ith failure.
(c) Using
(a) and
(b) argue that P{T1 +· · ·+Tj ≤ t} = (1− e
−λt )j
(d) Use
(c) to obtain P1j (t) = (1 − e
−λt )j−1 − (1− e
−λt )j = e
−λt (1 −e
−λt )j−1 and hence, given X(0) = 1,X(t) has a geometric distribution with parameter p = e
−λt .
(e) Now conclude that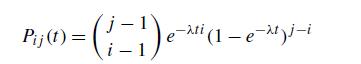
Step by Step Answer:







