For any event A, we define the random variable I {A}, called the indicator variable for A, by letting it equal 1 when A occurs and 0 when A does not. Now, if X(t) is a nonnegative random variable for all t ≥ 0, then it follows from a result in real analysis called Fubini’s theorem tha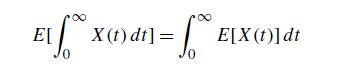

Suppose that X is a nonnegative random variable and that g is a differentiable function such that g(0) = 0.

(a) Show that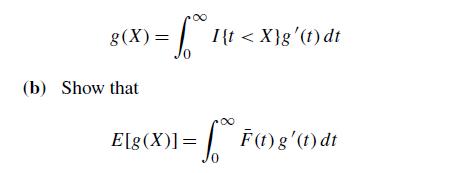

where ¯ F(t) = 1−F(t) = P(X >t).

(c) Show that E[X] = ∞
0 ¯ F(t)dt.

(d) Show that E[X2] = 2 ∞
0 t ¯ F(t)dt.

Transcribed Image Text:

E[ X(t) dt] = = La E[X(t)]dt 0