In Example 7.20, let denote the proportion of passengers that wait less than x for a

In Example 7.20, let π denote the proportion of passengers that wait less than x for a bus to arrive. That is, with Wi equal to the waiting time of passenger i, if we define

then π = limn→∞
n i=1Xi.

(a) With N equal to the number of passengers that get on the bus, use renewal reward process theory to argue that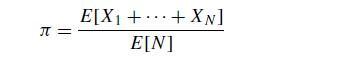

(b) With T equal to the time between successive buses, determine E[X1 +
· · ·+XN|T = t ].

(c) Show that E[X1 +· · ·+XN] = λE[min(T , x)].

(d) Show that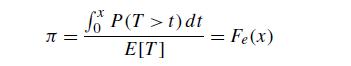

(e) Using that Fe(x) is the proportion of time that the excess of a renewal process with interarrival times distributed according to T is less than x, relate the result of

(d) to the PASTA principle that “Poisson arrivals see the system as it averages over time”.

Transcribed Image Text:

Xi 11 1, 10, if Wi