Let Y denote an exponential random variable with rate that is independent of the continuous-time Markov

Let Y denote an exponential random variable with rate λ that is independent of the continuous-time Markov chain {X(t)} and let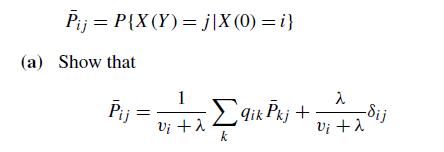

where δij is 1 when i = j and 0 when i = j .

(b) Show that the solution of the preceding set of equations is given by

where ¯P is the matrix of elements ¯ Pij , I is the identity matrix, and R the matrix specified in Section 6.9.

(c) Suppose now that Y1, . . . , Yn are independent exponentials with rate λ
that are independent of {X(t)}. Show that

is equal to the element in row i, column j of the matrix ¯ Pn.

(d) Explain the relationship of the preceding to Approximation 2 of Section 6.9.

Transcribed Image Text:

Pij= P{X(Y)=j|X (0) = i} (a) Show that Pij = 1 j + vi + 9ik Pk j k vi +2 -Sij