A biological medium consists of two substances 1 and 2 of densities n₁ and n₂. This medium is generating both substances by processes characterised by the matter source densities π₁ (n₁, n₂) and π₂ (n₁, n₂). The substances 1 and 2 can diffuse inside this medium. The matter current densities j₁ and j₂ follow Fick’s law (11.51),where D₁ > 0 and D₂ > 0 are the homogeneous diffusion constants of substances 1 and 2. The medium has a fixed volume, which means that its expansion rate vanishes, i.e. ∇· v = 0. Thus, the matter continuity equations for substances 1 and 2 are given by,At equilibrium, the system is assumed to be homogeneous and characterised by the densities n₀₁ and n₀₂ of substances 1 and 2. In the neighbourhood of the equilibrium, the matter source densities π₁ (n₁, n₂) and π₂ (n₁, n₂) are given to first-order in terms of the density perturbations Δ_n1 = n₁ − n₀₁ and Δ_n2 = n₂ − n₀₂ by,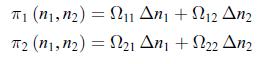where the coefficients Ω11, Ω12, Ω21, Ω22 are given by,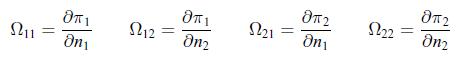Assume that the processes to generate substances 1 and 2 are the two chemical reactions 1  2 and 21 described by the stoichiometric coefficients ν_a1 = −1, ν_a2 = 1, ν_b1 = 1, ν_b2 = −1 and the reaction rate densities ω_a and ω_b. Assume that the temperature T and the chemical potentials μ₁ and μ₂ are homogeneous, i.e. ∇_T = 0 and ∇_μ1 = ∇_μ2 = 0. Analyse the evolution of the density perturbations Δ_n1 and Δ_n2 by using the following instructions:

a) Express the coefficients Ω11, Ω12, Ω21, Ω22 in terms of the total density n = n₁ + n₂, the density perturbations Δn₁ and Δn₂, the temperature T and a scalar W ≥ 0, which is a linear combination of Onsager matrix elements L_aa, L_ab, L_ba and L_bb. Begin by using the second law, i.e. πs ≥ 0, and the relation (8.68) for a mixture of ideal gas.

b) Determine the coupled time evolution equations for the density perturbations Δn₁ and Δn₂.c) Show that under the condition imposed in a) the relation,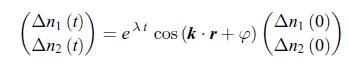is a solution of the coupled time evolution equations with λ

Transcribed Image Text:

j₁ = - D₁ Vn₁ and j2 = - D₂ Vn₂