A heat exchanger is made up of two identical pipes separated by an impermeable diathermal wall of
Question:
A heat exchanger is made up of two identical pipes separated by an impermeable diathermal wall of section area A, thickness h and thermal conductivity κ. In both pipes, a liquid flows at uniform velocities v1 = v1 ˆx and v2 = −v2 ˆx, with v1 > 0 and v2 > 0, where ˆx is the unit vector that is parallel to the liquid flow in pipe 1. The temperature T1 of the liquid in pipe 1 is larger than the temperature T2 of the liquid in pipe 2, i.e. T1 > T2. Thus, there is a heat current density jQ = jQˆy, with jQ > 0 going across the wall separating the pipes, where ˆy is the unit vector orthogonal to the wall and oriented positively from pipe 1 to pipe 2. There is no liquid current density across the wall, i.e. jC = 0. Heat conductivity is considered negligible in the direction of the flow and yet large enough to ensure a homogeneous temperature across any section of both pipes. Consider that the heat exchanger has reached a stationary state.a) Show that the temperature profiles in the fluids are given by the differential equations,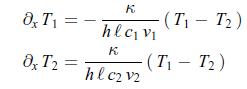 where c1 and c2 are the specific heat densities of liquids 1 and 2, and κ is the thermal conductivity of the diathermal wall and is a characteristic length for the thermal transfer.b) Show that the convective heat current density j = c1 v1 T1 + c2 v2 T2 is homogeneous.c) Determine the temperature difference ΔT (x) = T1 (x) − T2 (x).
where c1 and c2 are the specific heat densities of liquids 1 and 2, and κ is the thermal conductivity of the diathermal wall and is a characteristic length for the thermal transfer.b) Show that the convective heat current density j = c1 v1 T1 + c2 v2 T2 is homogeneous.c) Determine the temperature difference ΔT (x) = T1 (x) − T2 (x).
d) Determine the temperature profiles T1 (x) and T2 (x).e) Show that on a distance that is short enough, i.e. x/d 1,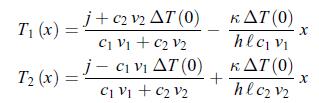
Step by Step Answer:

Principles Of Thermodynamics
ISBN: 9781108426091
1st Edition
Authors: Jean-Philippe Ansermet, Sylvain D. Brechet





