In electrochemistry, the observed current is generally determined by ion diffusion in the electrolyte. It was found
Question:
In electrochemistry, the observed current is generally determined by ion diffusion in the electrolyte. It was found that diffusion-limited currents can be avoided by using very small electrodes, known as ‘ultramicroelectrodes’ [192, 193, 194]. In order to capture how conductive current densities (also called diffusion current densities) vary with the size of the electrode, consider a spherical electrode and a conductive matter current density with spherical symmetry, jA = jAr ˆr ≡ jr ˆr. Show that when the system reaches a stationary state, the conductive matter current density is nonzero. The analysis of the transient behaviour would show that the stationary state is reached faster when the electrode is smaller. [195] In spherical coordinates (r, θ, φ), taking into account the spherical symmetry of the conductive matter current density, i.e. ∂/∂θ = 0 and ∂/∂φ = 0, the matter diffusion equation (11.54) for a solute of concentration c (r, t) reads,
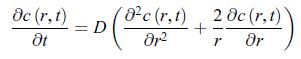
The boundary conditions are,![]() where c∗ is the concentration very far away from the electrode and r0 is the radius of the electrode. According to relation (11.51), the conductive matter current density scalar jr that characterises this electrode is,
where c∗ is the concentration very far away from the electrode and r0 is the radius of the electrode. According to relation (11.51), the conductive matter current density scalar jr that characterises this electrode is,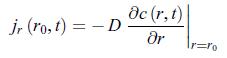
Establish the following results:a) The diffusion equation recast in terms of the function w(r, t) = r c (r, t) has the structure of a diffusion equation where the spherical coordinate r plays an analogous role to a Cartesian coordinate.b) The diffusion equation,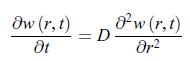 admits the solution,
admits the solution, First, write w(r, t) = f (η) where the variable η is a dimensionless function of r and t given by,
First, write w(r, t) = f (η) where the variable η is a dimensionless function of r and t given by, c) In the limit where the radius of the electrode is negligible, i.e. r = 0, the scalar conductive matter current density is given by,
c) In the limit where the radius of the electrode is negligible, i.e. r = 0, the scalar conductive matter current density is given by,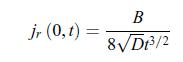 d) After a transient behaviour, the scalar conductive matter current density reaches a stationary value,
d) After a transient behaviour, the scalar conductive matter current density reaches a stationary value,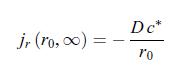
Step by Step Answer:

Principles Of Thermodynamics
ISBN: 9781108426091
1st Edition
Authors: Jean-Philippe Ansermet, Sylvain D. Brechet





