The surface tension modifies the melting point of particles. The effect is important when the diameter is in the nanometer range. A differential equation has to be written for Tm (r), the melting temperature of particles of radius r. In order to perform this thermodynamical analysis, assume that the pressure ps inside the particles is defined [67]. At atmospheric pressure p0 and for infinitely large particles, the melting temperature is noted T∞. The surface tension is γs for a solid particle and γl for a liquid one. According to exercise 4.8, the Laplace pressure ps (r) for a solid nanoparticle and the Laplace pressure p (r) for a liquid nanoparticle are given by,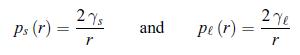

Determine the temperature difference T∞ − Tm (r) in terms of the latent heat of melting s = T∞ (s − ss) and the molar volumes vs and v that are both assumed to be independent of the radius r. Therefore, perform a series expansion in terms of the radius r on the chemical equilibrium condition. This result is known as the Gibbs–Thomson equation. For some materials, a lowering of the melting temperature can be expected, i.e. Tm (r)

Transcribed Image Text:

Ps (r): = 27s r and pe (r): 27e r