Two long blocks, made up of different homogeneous materials, are at temperatures T₁ and T₂ when they are brought into contact with one another. The interface quickly reaches a temperature T₀ given by, 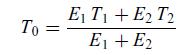where E₁ =√κ₁ c₁ > 0 and E₂ = √κ₂ c₂ > 0 are called the effectivities of materials 1 and 2, where κ₁ and κ₂ are the thermal conductivities and c₁ and c₂ the specific heat per unit volume of both materials. If material 1 is very hot, but it has a low thermal conductivity κ₁ and specific heat c₁, and to the contrary material 2 has large thermal conductivity κ₂ and specific heat c₂, then the temperature of the interface T₀ is almost T₂, i.e. material 2 does not ‘feel the heat’ of material 1. Establish this result by using the following instructions:

a) Consider an x-axis normal to the interface with x = 0 at the interface, x 0 in material 2. Let T₁ (x, t) and T₂ (x, t) be the solutions of the heat diffusion equation (11.35) in materials 1 and 2. Determine the boundary conditions on T₁ (x, t) and T₂ (x, t) at the interface.

b) Using an approach that is analogous to the one presented in § 11.4.3, show that the general solutions for the temperature profiles T₁ (x, t) and T₂ (x, t) are given by,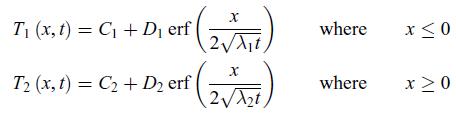

where erf (ν) is the error function defined as,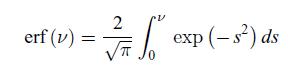and C₁, C₂, D₁ and D₂ are constant coefficients.

c) Use the boundary conditions to determine the coefficients in terms of the temperatures T₀, T₁ and T₂. Show that the temperature T₀ is given by the effusivity relation just after the two blocks have reached a common temperature at the interface.

Transcribed Image Text:

To E₁ T₁ + E₂ T₂ E₁ + E2