Obtain the transition matrix for the gambler's ruin problem discussed earlier.

From the given information, it can be seen that there are five states viz. Rs 0, Rs 10, Rs 20, Rs 30, and Rs 40. From all the states, except the states of Rs O and Rs 40, we know that the person would be in the next state (with Rs IO more) with a probability ofp, and in the previous state (with Rs IO less) with a probability of 1 - p. Of course, if the person reaches the state of Rs O or Rs 40, then he does not play the game anymore. In such a case, the state does not change. Hence, for each of these states, the transition probability would be equal to l. Accordingly, p00 = p 44 = l.

The transition probabilities are contained in Table 14.2.

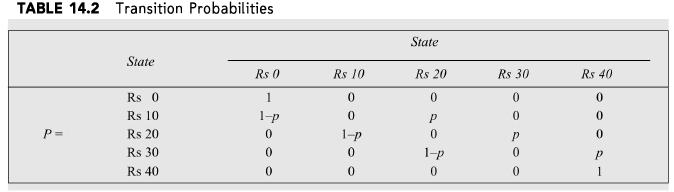
TABLE 14.2 Transition Probabilities State State Rs 0 Rs 10 Rs 20 Rs 30 Rs 40 Rs 0 1 0 0 0 0 Rs 10 1-p 0 P 0 0 P= Rs 20 0 1-p 0 P 0 Rs 30 0 1-p Rs 40 0 0 Po 0 P 0 1