Suppose a telephone company had two kinds of customers. One had a utility function that could be represented as u1(x) = 5x - x2 - 5(x), where x is the total amount of time spent on the phone and k is the total cost to the customer for service. This results in a marginal utility curve ˆ‚ u1(x) ˆ‚x = 5 - 2x - ˆ‚k/ˆ‚x. The other type of consumer possesses a utility function that can be written as u2(x) = 5x - x2 - k(x) - x/k(x), resulting in a marginal utility curve

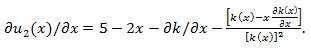
Suppose that each faces no budget constraint (so that they will purchase until marginal utility declines to zero). Suppose the firm charges a linear price so that k(x) = px, and marginal cost is given by ˆ‚k(x) / ˆ‚x = p. What is the demand curve for each customer type?

Transcribed Image Text:

ak(x) ax du2(x)/ax = 5- 2x - ak/ax [k (x)]?