The circuit representation in the chapter is more detailed than necessary if we care only about Circuit functionality. A simpler formulation describes any rn-input, n-output gate or circuit using a predicate with m + n arguments, such that the predicate is true exactly when the inputs and outputs are consistent. For example, NOT-gates are described by the binary predicate NOT (i, o), for which NOT (0, 1) and NOT (1, 0) are known. Compositions of gates are defined by conjunctions of gate predicates in which shared variables indicate direct connections. For example, a NAND circuit can be composed from ANDs and NOTs: Using this representation define the one-bit adder in Figure and the four-hit adder in Figure, and explain what queries you would use to verify the designs. What kinds of queries are not supported by this representation that is supported by the representation in Section8.4?

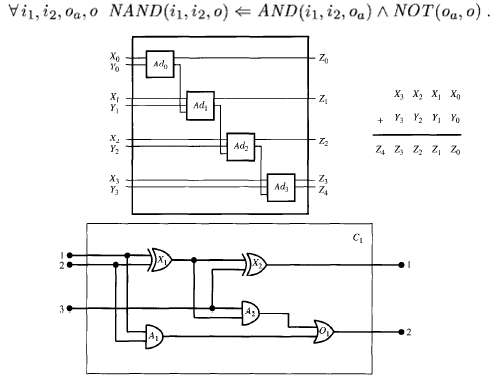
AND(i1, i2, 0a) A NOT(0a, 0). NAND(i1, i2, 0) Vi1, i2, 0a, 0 Ad, Yo , , , , Ad, + Y, Y, Y, Yo Ad, Y2 Adz Z4 Y3 A: