The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in unbounded conducting media has

Question:

The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in unbounded conducting media has a solution to the initial value problem ?of the form,

A(x, t) = ? d³x' G(x - x', r)A(x', 0)

where A(x', 0) describes the initial field configuration and G is an appropriate kernel.

(a) Solve the initial value problem by use of a three-dimensional Fourier transform in space for A(x, t). With the usual assumptions on interchange of orders of integration, show that the Green function has the Fourier representation,

and it is assumed that t > 0.(b) By introducing a Fourier decomposition in both space and time, and performing the frequency integral in the complex ?? plane to recover the result of part a, show that G(x-x', t) is the diffusion Green function that satisfies the inhomogeneous equation,

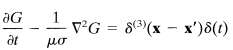
and vanishes for t (c) Show that if a is uniform throughout all space, the Green function is

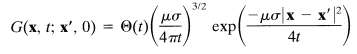
(d) Suppose that at time t' = 0, the initial vector potential A(x', 0) is nonvanishing only in a localized region of linear extent d around the origin. The time dependence of the fields is observed at a point P far from the origin, i.e., | x | = r >> d. Show that there are three regimes of time, 0 1,??₁ ? t ? T₂, and t >> T₂. Give plausible definitions of T₁ and T₂, and describe qualitatively the time dependence at P. Show that in the last regime, the vector potential is proportional to the volume integral of A(x', 0) times t^-3/2, assuming that integral exists. Relate your discussion to those of Section 5.18.B and Problems 5.35 and 5.36.