The magnetic field outside a long straight wire carrying a steady current 1 is (of course) The electric field inside the wire is uniform: wherepis the resistivity and a is the radius (see Exs. 7.1 and 7.3). Question: What is the electric field outside the wire? This is a famous problem, first analyzed by Sommerfeld, and known in its most recent incarnation as "Merzbacher's puzzle."²²The answer depends on how you complete the circuit. Suppose the current returns along a perfectly conducting grounded coaxial cylinder of radius b (Fig. 7.55). In the region a < s < b, the potential V(s, z) satisfies Laplace's equation, with the boundary conditions Unfortunately, this does not suffice to determine the answer--we still need to specify boundary conditions at the two ends. In the literature it is customary to sweep this ambiguity under the rug by simply asserting (in so many words) that V(s, z) is proportional to z: V(s, z) = zf(s). On this assumption: 

(a) Determine V (s, z). 

(b) Find E(s, z). 

(c) Calculate the surface charge density σ(z) on the wire.

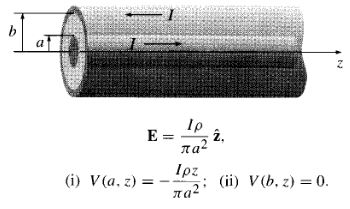
Ip , E = ? Ipz (i) V(a, z) = (ii) V(b, ) 0.