The potential energy of a mass m as a function of position is given by U(x) =
Question:
The potential energy of a mass m as a function of position is given by U(x) = U0(a + 1/a), where a = x/a and a is a constant.
(a) Plot U(x) versus x for 0.1a < x < 3a.
(b) Find the value of x = x0 at stable equilibrium.
(c) Write the potential energy U(x) for x = x0 + ε, where ε is a small displacement from the equilibrium position x0.
(d) Approximate the 1/x term using the binomial expansion with r = ε/x0 << 1 and discarding all terms of power greater than r2.
(e) Compare your result with the potential for a simple harmonic oscillator. Show that the mass will undergo simple harmonic motion for small displacements from equilibrium and determine the frequency of this motion.
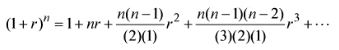
Step by Step Answer:

Fundamentals of Ethics for Scientists and Engineers
ISBN: 978-0195134889
1st Edition
Authors: Edmund G. Seebauer, Robert L. Barry





