The quantity B used in ratio estimation is sometimes called the ratio-of-means estimator. An alternative that has

The quantity ˆB used in ratio estimation is sometimes called the ratio-of-means estimator.

An alternative that has been proposed is the mean of ratios estimator: Let b_i = y_i/x_i for unit i; then the mean-of-ratios estimator is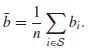

a. Do you think the mean-of-ratios estimator is appropriate for the data in Example 4.5? Why, or why not?

b. Show that, for the ratio-of-means estimator ˆB, tx ˆB = t_y when the entire population is sampled (i.e., S = U).

c. Define

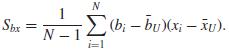
Show that for an SRS of size n, the bias of as an estimator of B is

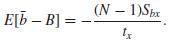
As a consequence, if S_bx ≠ 0 the bias does not decrease as n increases.

d. (Requires linear model theory.) Show that is the weighted least squares estimator of β under the model

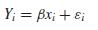
When ε_i’s are independent with mean 0 and variance σ²x²_i .

Transcribed Image Text:

She = NT i=1 (N -1)Shr