This exercise is based on results in Brewer and Donadio (2003). a Show, using the results in
Question:
This exercise is based on results in Brewer and Donadio (2003).
a Show, using the results in Theorem 6.1, that the variance in (6.21) can be rewritten as:
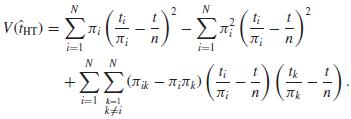
Write t i / πi − tk / πk = ti / πi – t / n + t / n − tk / πk .
b The first term in (6.47) is the variance that would result if a with replacement sample with selection probabilities ψi = πi / n were taken. Brewer and Donadio (2003) suggest that the second term may be viewed as a finite population correction for unequal-probability sampling, so that the first two terms in (6.47) approximate V(ṫHT) without depending on the joint inclusion probabilities πik . Calculate the three terms in (6.47) for an SRS of size n.
c Suppose that there exist constants ci such that πik ≈ πiπk(ci + ck)/2. Show that with this substitution, the third term in (6.47) can be approximated by
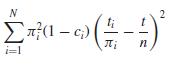
so that
Two choices suggested for ci are ci = (n −1) / (n −πi) or (following Hartley and
Rao, 1962),
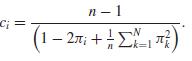
Step by Step Answer:
a From 621 From Theorem 61 we know that And So This gives the first two terms in 647 the third te...View the full answer
