Two distances are required to specify the location of a point relative to an origin in two-dimensional space (Figure):

• The horizontal and vertical distances ( x . y ) in Cartesian coordinates
• The radius and angle (r, θ) in radial coordinates.

It is relatively straightforward to compute Cartesian coordinates (x, y) on the basis of polar coordinates (r, θ). The reverse process is not so simple. The radius can be computed by the following formula: r = √ x² + y²

If the coordinates lie within the first and fourth coordinates (i.e., x > 0), then a simple formula can be used to compute θ

θ = tan – 1 (y/x)

The difficulty arises for the other cases. The following table summarizes the possibilities:

(a) Write a well-structured flowchart for a subroutine procedure to calculate r and θ as a function of x and y. Express the final results for θ in degrees.

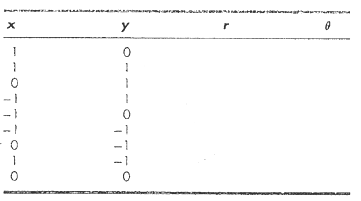
(b) Write a well-structured function procedure based on your flowchart. Test your program by using it to fill out following table:

IV II