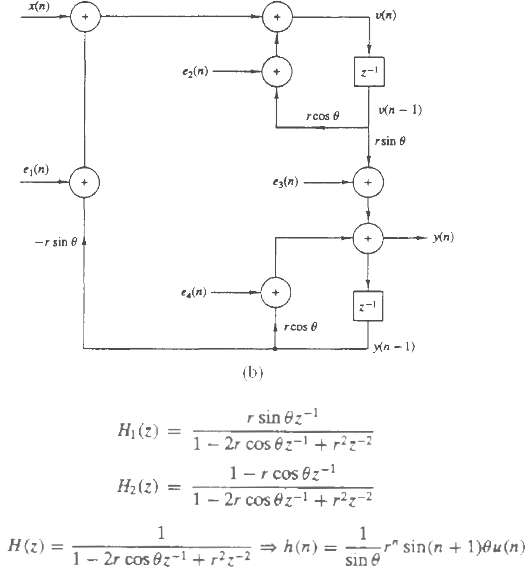
Shown in Figure is the coupled-form implementation of a two-pole filter with poles at x = re^?j0. There are four real multiplications per output point. Let ei(n), i = 1, 2, 3, 4 represent the round-off noise in fixed-point implementation of the filter. Assume that the noise sources are zero-mean mutually uncorrelated stationary white noise sequences. For each n the probability density function p(e) is uniform in the range -?/2 ? e ? ?/2, where ? = 2^-b.

(a) Write the two coupled difference equations for y(n) and v(n), including the noise sources and the input sequence x(n)

(b) From these two difference equations, show that the filter system function H₁(z) and H₂(z) between the input noise terms e₁(n) + e₂(n) and e₃(n) + e₄(n) and the output y(n) are:

We know that

Determine h₁(n) and h₂(n).

(c) Determine a closed-form expression for the variance of the total noise from e_i(n), i = 1, 2, 3, 4 at the output of the filter.

(n) un) ez(n) v(n - 1) rcos e rsin 8 e,(n) ez(n) Mn) -r sin e esin) Xn - 1) (b) r sin 6z- 1- 2r cos 6z- + riz-2 1-r cos 6z-1 1- 2r cos ez- + pz-2 H(2) H2(z) " sin(n + 1)eu (n) sin e H(z) = = h(n) = - 1- 2r cos 0z-1 + r?z-2