(a) Construct the free-space Green function G(x, ?; ??, ?') for two-dimensional electrostatics by integrating 1/R with respect to (z? - z) between the limits ?Z, where Z is taken to be very large. Show that apart from an inessential constant, the Green function can be written alternately as

G(x, y; x?, y') = ?ln[(x - x')² + (y ? y')²]

= ?ln[?² + ?'² ? 2??' cos(? ? ?')]

(b) Show explicitly by separation of variables in polar coordinates that the Green function can be expressed as a Fourier series in the azimuthal coordinate,

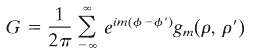
Where the radial Green functions satisfy

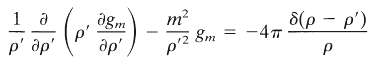
Note that g_m(?, p') for fixed p is a different linear combination of the solutions of the homogeneous radial equation (2.68) for ?' ?, with a discontinuity of slope at ?' = ? determined by the source delta function.

(c) Complete the solution and show that the free-space Green function has the expansion

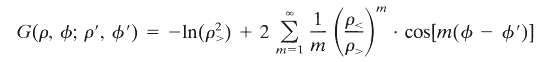
Where p_{(p>) is the smaller (larger) of p and p'.}

E eim(a -d"gm(P, p') 2 T