A Realistic Version of the Twin Paradox A rocket ship leaves the earth on January 1, 2100.
Question:
A Realistic Version of the Twin Paradox A rocket ship leaves the earth on January 1, 2100. Stella, one of a pair of twins born in the year 2015, pilots the rocket (reference frame S'); the other twin, Terra, stays on the earth (reference frame S). The rocket ship has an acceleration of constant magnitude g in its own reference frame (this makes the pilot feel at home, since it simulates the earth's gravity). The path of the rocket ship is a straight line in the +x-direction in frame S.(a) Using the results of Challenge Problem 37.73, show that in Terra's earth frame S, the rocket's accelerations where u is the rocket's instantaneous velocity in frame S.(b) Write the result of part (a) in the form dt = f (u) du, where f (u) is a function of u, and integrate both sides. Show that in Terra's frame, the time when Stella attains a velocity v1x is(c) Use the time dilation formula to relate dt and dt' (infinitesimal time intervals measured in frames S and S', respectively). Combine this result with the result of part (a) and integrate as in part (b) to show the following: When Stella attains a velocity v1x relative to Terra, the time that has elapsed in frame S' is Here arc tanh is the inverse hyperbolic tangent.(d) Combine the results of parts (b) and (c) to find t1, in terms of t1, g, and c alone.(e) Stella accelerates in a straight-line path for five years (by her clock), slows down at the same rate for five years, turns around, accelerates for five years, slows down for five years, and lands back on the earth. According to Stella's clock, the date is January 1, 2120. What is the date according to Terra'sclock?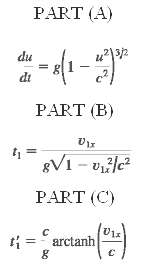
Step by Step Answer:






