A: Suppose further that both technologies take capital k and labor as inputs but that the

Question:

A: Suppose further that both technologies take capital k and labor ℓ as inputs but that the patented technology is more capital intensive.

(a) Draw two isoquants, one from the technology representing the less capital intensive and one representing the more capital intensive technology. Then illustrate the slice of each map that a firm will choose to operate on assuming the wage w and rental rate r are the same in each case.

(b) Suppose that the patented technology is sufficiently advanced such that, for any set of input prices, there always exists an output level at which it is (long run) cost effective to switch to this technology. On a graph with output x on the horizontal and dollars on the vertical, illustrate two cost curves corresponding to the two technologies and then locate x̅. Then illustrate the cost curve that takes into account that a firm will switch to the patented technology at x̅.

(c) What happens to x̅ if the license cost F for using the patented technology increases? Is it possible to tell what happens if the capital rental rate r increases?

(d) At x̅, which technology must have a higher marginal cost of production? On a separate graph, illustrate the marginal cost curves for the two technologies.

(e) At x̅, the firm is cost-indifferent between using the two technologies. Recognizing that the marginal cost curves capture all costs that are not fixed — and that total costs excluding fixed costs can be represented as areas under marginal cost curves, can you identify an area in your graph that represents the recurring fixed license fee F?

(f) Suppose output price p is such that it is profit maximizing under the non-patented technology to produce x̅. Denote this as P̅. Can you use marginal cost curves to illustrate whether you would produce more or less if you switched to the patented technology?

(g) Would profit be higher if you used the patented or non-patented technology when output price is P̅. (Identify the total revenues if the firm produces at P̅ under each of the technologies. Then identify the total cost of using the non-patented technology as an area under the appropriate marginal cost curve and compare it to the total costs of using the patented technology as an area under the other marginal cost curve and add to it the fixed fee F.)

(h) True or False: Although the total cost of production is the same under both technologies at output level x̅, a profit maximizing firm will choose the patented technology if price is such that x̅ is profit maximizing under the non-patented technology.

(i) Illustrate the firm’s supply curve.

B: Suppose that the two technologies available to you can be represented by the production functions f (ℓ,k) = 19.125ℓ^0.4 k^0.4 and g(ℓ,k) = 30ℓ^0.2 k^0.6, but technology g carries with it a recurring fee of F.

(a) In exercise 13.2 you derived the general form for the 2-input Cobb-Douglas conditional input demands and cost function.¹ Use this to determine the ratio of capital to labor (as a function of w and r) used under these two technologies. Which technology is more capital intensive?

(b) Determine the cost functions for the two technologies (and be sure to include F where appropriate).

(c) Determine the output level x̅ (as a function of w, r and F) at which it becomes cost effective to switch from the technology f to the technology g. If F increases, is it possible to tell whether x̅ increases or decreases? What if r increases?

(d) Suppose w = 20 and r = 10. Determine the price P̅ (as a function of F) at which a firm using technology f would produce x̅.

(e) How much would the firm produce with technology g if it faces P̅? Can you tell whether, regardless of the size of F, this is larger or smaller than x̅ (which is the profit maximizing quantity when the firm used technology f and faces P̅)?

(f) The (long run) profit function for a Cobb-Douglas production function f (ℓ,k) = Aℓ^αk^β is

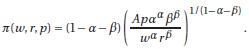
Can you use this to determine (as a function of p,w and r) the highest level of F at which a Profit maximizing firm will switch from f to g? Call this F̅ (w,r,p).

(g) From your answer to (f), determine (as a function of w, r and F) the price p∗ at which a profit maximizing firm will switch from technology f to technology g.

(h) Suppose again that w = 20, r = 10. What is p∗ (as a function of F)? Compare this to P̅ you calculated in part (d) and interpret your answer in light of what you did in A(i).

(i) Suppose (in addition to the values for parameters specified so far) that F = 1000. What is P̅ and p∗? At the price at which the profit maximizing firm is indifferent between using technology f and technology g, how much does it produce when it uses f and how much does it produce when it uses g?²

(j) Continuing with the values we have been using (including F = 1000), can you use your answer to (a) to determine how much labor and capital the firm hires at p∗ under the two technologies? How else could you have calculated this?

(k) Use what you have calculated in (i) and (j) to verify that profit is indeed the same for a firm whether it uses the f or the g technology when price is p^∗ (when the rest of the parameters of the problem are as we have specified them in (i) and (j).)