Decide which of the following statements are true and which are false. Prove the true ones and provide counterexamples for the false ones.

a) If x_n is strictly decreasing and 0 < x_n < 1/2, then x_n → 0 as n → ∞.

b) If

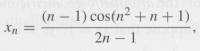
then x_n has a convergence subsequence.

c) If x_n is a strictly increasing sequence and |x_n| < 1 + 1/n for n = 1,2,..., then x_n → 1 as n → ∞.

d) If x_n has a convergent subsequence, then x_n is bounded.

Transcribed Image Text:

(n - 1) costn 1) 2n - 1