Flow near a wall suddenly set in motion (approximate solution) (Fig. 4B.2). Applu procedure like that of
Question:
Flow near a wall suddenly set in motion (approximate solution) (Fig. 4B.2). Applu procedure like that of Example 4.4-1 to get an approximate solution for Example 4.1.1
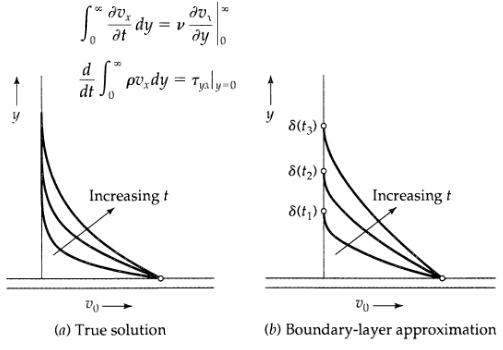
(a) Integrate Eq. 4.4-1 over y to get make use of the boundary conditions and the Leibniz rule for differentiating an integral (Eq. C.3-2) to rewrite Eq. 4B.2-1 in the form Interpret this result physically.
(b) We know roughly what the velocity profiles look like. We can make the following reasonable postulate for the profiles: Here S(t) is a time-dependent boundary-layer thickness. Insert this approximate expression into Eq. 4B.2-2 to obtain
(c) Integrate Eq. 4B.2-5 with a suitable initial value of S(t), and insert the result into Eq. 4B.2-3 to get the approximate velocity profiles.
(d) Compare the values of v,/v∞ obtained from (c) with those from Eq. 4.1-15 at y/√4vt = 0.2, 0.5, and 1.0. Express the results as the ratio of the approximate value to the exact value.
Step by Step Answer:
PS dt 20x dz t Flow near a wall suddenly set in motion approxim...View the full answer
