Flow of a fluid with a suddenly applied constant wall stress, in the system studied in Example 4.1-1, let the fluid be at rest before t = 0. At time t = 0 a constant force is applied to the fluid at the wall in the positive x direction, so that the shear stress τ_yx takes on a new constant value τ₀ at y = 0 for t > 0. 

(a) Differentiate Eq. 4.1-1 with respect to y and multiply by - μ to obtain a partial differential equation for τ_yx(y, t). 

(b) Write the boundary and initial conditions for this equation. 

(c) Solve using the method in Example 4.1-1 to obtain 

(d) Use the result in (c) to obtain the velocity profile. The following relation¹ will be helpful

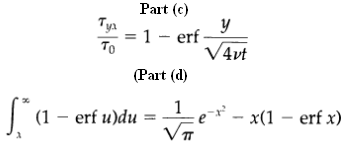
Part (c) = 1 - erf- TO V4vt (Part (d) (1 erf u)du = VT x(1 erf x)