In computing the DFT, it is necessary to multiply a complex number by another complex number whose magnitude is unity, i.e., (X + jY) e ^j?. Clearly, such a complex multiplication changes only the angle of the complex number, leaving the magnitude unchanged. For this reason, multiplications by a complex number e ^j??are sometimes called rotations. In DFT or FFT algorithm, many different angles ? may be needed. However, it may be undesirable to store a table of all required values of sin ? and cos ?, and computing these functions by a power series requires many multiplications and additions. With the CORDIC algorithm given by Volder (1959), the product (X + jY) e^j??can be evaluated efficiently by a combination of additions, binary shifts, and table lookups from a small table.

?(a) Define ?_i = arctan (2^??i). Show that any angle 0 i = ? 1 and the error ? is bounded by |?| ? arctan (2 ^?M).

(b) The angles ?_i may be computed in advance and stored in a small table of length M. State an algorithm for obtaining the sequence {a_i} for i = 0, 1, ?, M ? 1, such that a_i = ? 1. Using your algorithm to determine the sequence {a_i} for representing the angle ? = 100 ?/512 when M = 11.

(c) Using the result of part (a), show that the recursion, will produce the complex number (X_M + jY _M) = (X + jY) G_Me^j?, where ? = ?^M?1_i=0 a_i ?_i and G_M is real, is positive, and does not depend on ?. That is, the original complex number is rotated in the complex plane by an angle ? and magnified by the constant G_M.

(d) Determine the magnification constant G_M as a function of M.

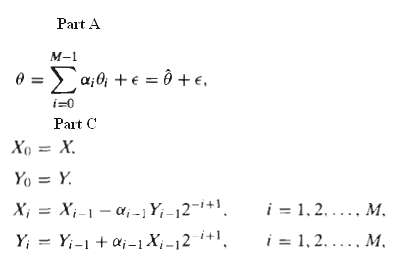
Part A M-1 a;0; + = 0 +e, 0 = i=0 Pait C Xo = X. Yo = Y. X; = X;-1 - a, -Y-12-i+1. i = 1,2..... M. i = 1, 2.... M, Y; = Y;-1 + a;-1X;-12 i+1.