In many applications (such as evaluating frequency responses and interpolation), it is of interest to compute the DFT of a short sequence that is ?zero-padded.? In such cases, a specialized ?pruned? FFT algorithm can be used to increase the efficiency of computation (Markel, 1971). In this problem, we will consider pruning of the radix-2 decimation-in-frequency algorithm when the length of the input sequence is M ? 2^u and the length of the DFT is N = 2^v, where u

(a) Draw the complete flow graph of a decimation-in-frequency radix-2 FFT algorithm for N = 16. Label all branches appropriately.

(b) Assume that the input sequence is of length M = 2; i.e., x[n] ? 0 only for N = 0 and N = 1. Draw a new flow graph for N = 16 that shows how the nonzero input samples propagate to the output DFT; i.e., eliminate or prune all branches in the flow graph of part (a) that represent operations non zero-inputs.

(c) In part (b), all of the butterflies in the first three stages of computation should have been effectively replaced by a half-butterfly of the form shown in Figure, and in the last stage, all the butterflies should have been of the regular form. For the general case where the length of the input sequence is M ? 2^u and the length of the DFT is N = 2^v, where u

Transcribed Image Text:

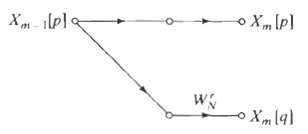
Xm - ilpl a Xml9)