On December 31, 2014, when the market interest rate is 6 percent, an investor purchases $700,000 of Tennis Bubbles Ltd. 10-year, 5-percent bonds at issuance for $647,929. Interest is paid semi-annually. Assume that the investor plans to hold the investment to maturity.

Disregard commissions.

Required

Prepare a schedule for amortizing the discount on the bond investment through December 31, 2015. The investor uses the effective-interest amortization method. Use Exhibit 15-4 on page 931 as a guide. Journalize the purchase on December 31, 2014, the first semiannual interest receipt on June 30, 2015, and the year-end interest receipt on December 31, 2015.

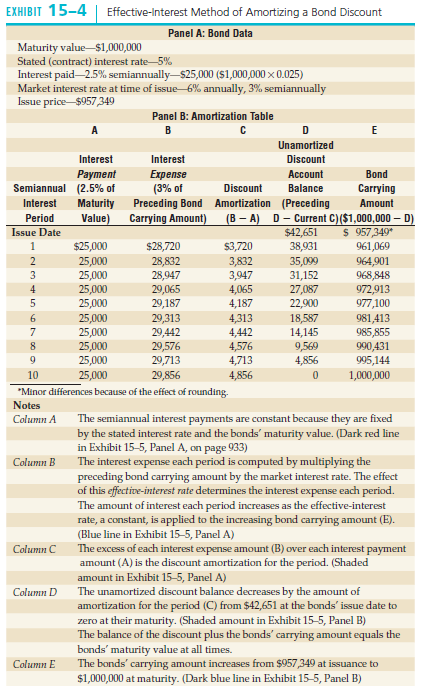
Transcribed Image Text:

EXHIBIT 15-4 | Effective-Interest Method of Amortizing a Bond Discount Panel A: Bond Data Maturity value–$1,000,000 Stated (contract) interest rate 5% Interest paid 2.5% semiannually$25,000 (S1,000,000 x 0.025) Market interest rate at time of issue- 6% annually, 3% semiannually Issue price $957,349 Panel B: Amortization Table Unamortized Interest Interest Discount Bond Carrying Payment Semiannual (2.5% of Expense (3% of Account Discount Balance Interest Maturity Preceding Bond Amortization (Preceding Value) Amount Carrying Amount) D- Current C)($1,000,000 – D) $ 957,349* 961,069 964,901 968,848 972,913 977,100 981,413 985,855 990,431 995,144 1,000,000 Period (B – A) Issue Date $42,651 $3,720 3,832 3,947 4,065 4,187 4,313 $25,000 $28,720 28,832 28,947 29,065 29,187 29,313 29,442 29,576 29,713 29,856 38,931 2 25,000 35,099 31,152 27,087 3 25,000 25,000 25,000 25,000 25,000 25,000 4 22,900 18,587 4,442 14,145 4,576 9,569 4,856 25,000 25,000 4,713 10 4,856 *Minor differences because of the effect of rounding. Notes The semiannual interest payments are constant because they are fixed by the stated interest rate and the bonds' maturity value. (Dark red line in Exhibit 15-5, Panel A, on page 933) The interest expense each period is computed by multiplying the preceding bond carrying amount by the market interest rate. The effect of this effective-interest rate determines the interest expense each period. The amount of interest each period increases as the effective-interest rate, a constant, is applied to the increasing bond carrying amount (E). (Blue line in Exhibit 15-5, Panel A) The excess of each interest expense amount (B) over each interest payment amount (A) is the discount amortization for the period. (Shaded amount in Exhibit 15-5, Panel A) The unamortized discount balance decreases by the amount of amortization for the period (C) from $42,651 at the bonds' issue date to Column A Column B Column C Column D zero at their maturity. (Shaded amount in Exhibit 15-5, Panel B) The balance of the discount plus the bonds' carrying amount equals the bonds' maturity value at all times. The bonds' carrying amount increases from $957,349 at issuance to $1,000,000 at maturity. (Dark blue line in Exhibit 15-5, Panel B) Column E