Introduction to Electrodynamics 3rd Edition David J. Griffiths - Solutions
Unlock the full potential of your studies with our comprehensive resource dedicated to "Introduction to Electrodynamics 3rd Edition" by David J. Griffiths. Dive into a treasure trove of knowledge with online solutions and an extensive answers key. Explore the solution manual and solutions PDF, providing solved problems and questions with answers tailored for your learning needs. Access the test bank and chapter solutions for a deeper understanding. Benefit from step-by-step answers and the instructor manual, all designed to complement your textbook. Enhance your learning experience with our free download options, ensuring you have all the tools for success.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


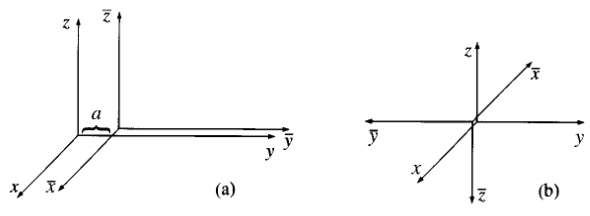

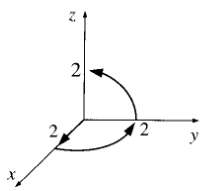

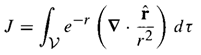
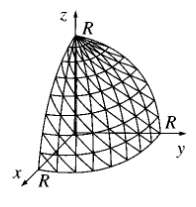

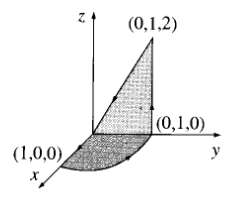

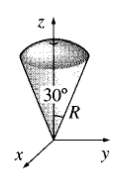
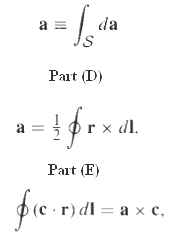
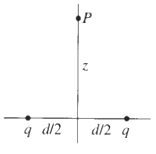
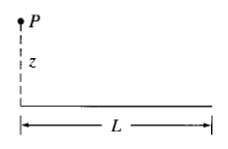
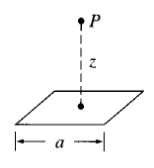
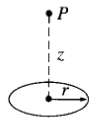
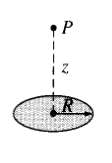
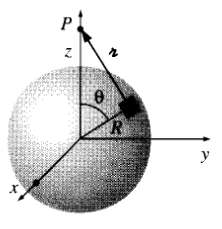
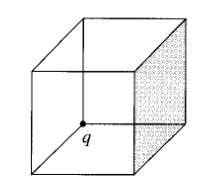
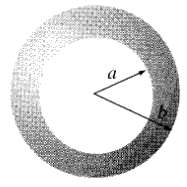

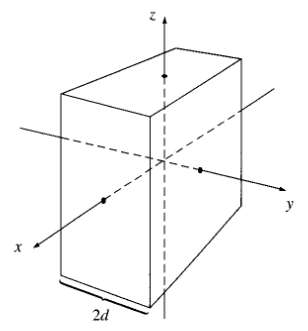
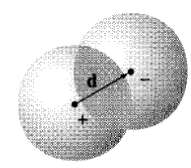
![E = k[xyx + 2yzŷ + 3xzî] È = k[y²& + (2æy+ z²)ŷ + 2yzî]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/9/7/9/3105c90956e5c6d51552979311581.jpg)