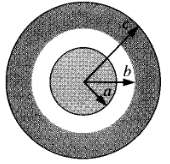
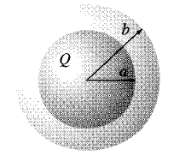
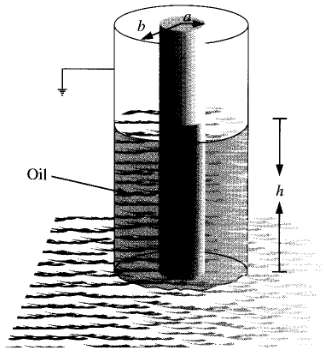
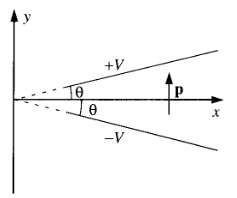
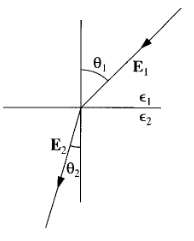
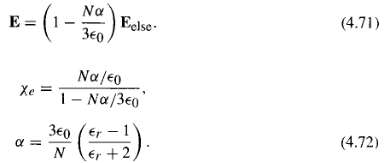![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



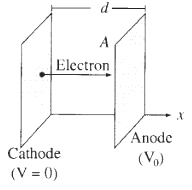
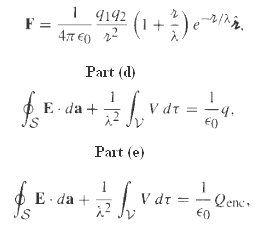
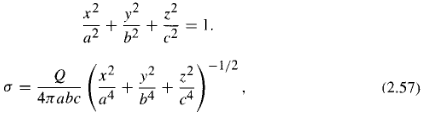
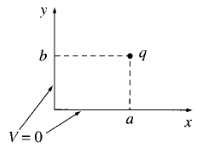
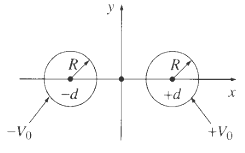
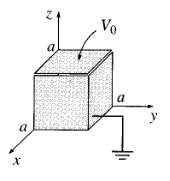
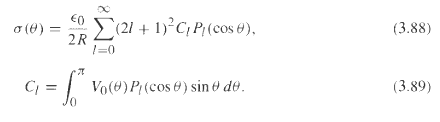
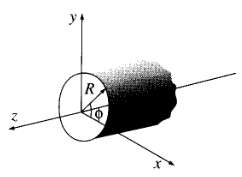
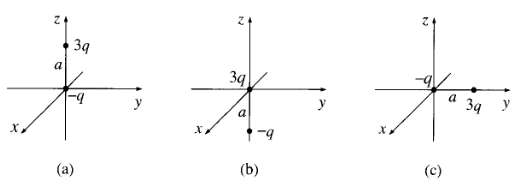

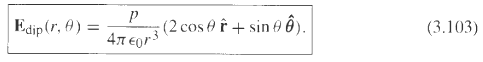
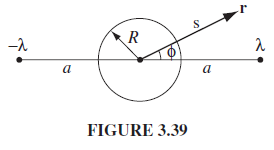
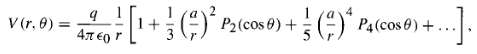
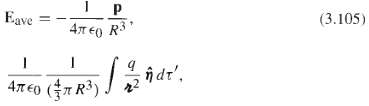
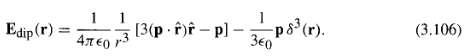
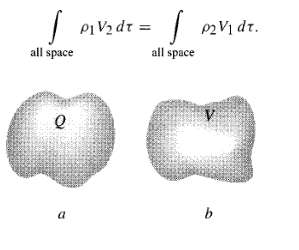

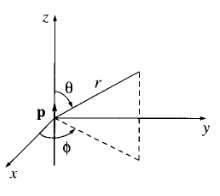
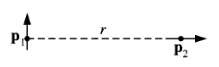
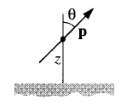
![[pI P2 - 3(P1 f)(p2 · f)]. (4.7) 4T €0 r3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/9/9/2/6305c90c976ae32a1552992631856.jpg)