Show that the average field inside a sphere of radius R, due to all the charge within the sphere, is where p is the total dipole moment. There are several ways to prove this delightfully simple result. Here's one method:

(a) Show that the average field due to a single charge q at point r inside the sphere is the same as the field at r due to a uniformly charged sphere with p = ? q/(4/3 ?R³), namely where ? is the vector from r to d?'.?

(b) The latter can be found from Gauss's law (see Prob. 2.12). Express the answer in terms of the dipole moment of q.?

(c) Use the superposition principle to generalize to an arbitrary charge distribution.?

(d) While you're at it, show that the average field over the sphere due to all the charges outside is the same as the field they produce at the center.

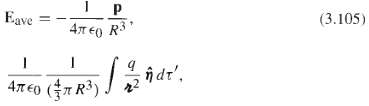
Eave 40 R 1 I Ameo (7R) dt', (3.105)