Recall that element a of a group G with identity element e has order r > 0
Question:
Recall that element a of a group G with identity element e has order r > 0 if ar = e and no smaller positive power of a is the identity. Consider the group S8.
a. What is the order of the cycle ( 1, 4, 5, 7)?
b. State a theorem suggested by part (a).
c. What is the order of a = (4, 5)(2, 3, 7)? of r = (1, 4)(3, 5, 7, 8)?
d. Find the order of each of the permutations given in Exercises 10 through 12 by looking at its decomposition into a product of disjoint cycles.
e. State a theorem suggested by parts (c) and (d).
Data from Exercise 10
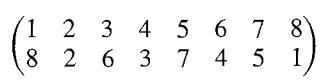
Data from Exercise 11

Data from Exercise 12
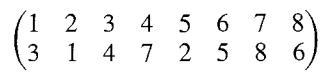
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





