(a) Now suppose that air resistance is a retarding force tangent to the path but acts opposite to the motion. If we take air resistance to be proportional to the velocity of the projectile, then we saw in Problem 24 of Exercises 4.9 that motion of the projectile is describe by the system of linear differential equations

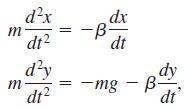
Where β > 0. Use the Laplace transform to solve this system subject to the initial conditions 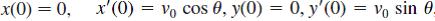 where 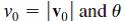are constant.

(b) Suppose slug 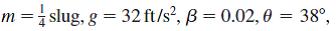 Use a CAS to find the time when the projectile hits the ground and then compute its corresponding horizontal range.

(c) Repeat part (c) using the complementary angle θ = 52° and compare the range with that found in part (b). Does the property in part (c) of Problem 49 hold?

(d) Use the parametric equations and in part (a) along with the numerical data in part (b) to plot the ballistic curve of the projectile. Repeat with the same numerical data in part (b) but take θ = 52°. Superimpose both curves on the same coordinate system. Compare these curves with those obtained in part (e) of Problem 49.

(reference exercise 4.9 of problem 24)

Exercise 4.9

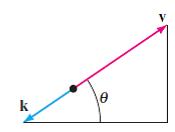
Determine a system of differential equations that describes the path of motion in Problem 23 if air resistance is a retarding force k (of magnitude k) acting tangent to the path of the projectile but opposite to its motion. See Figure 4.9.3. Solve the system. k is a multiple of velocity, say βv.

Transcribed Image Text:

x(0) = 0, x'(0) = Vo cos 0, y(0) = 0, y'(0) = vo sin 0. %3D